Descubre la estructura de los mosaicos de Escher

Si pinchas aquí, accederás  a la estupenda web del profesor navarro Manuel Sada y podrás descubrir cómo formó Escher algunos de sus magníficos mosaicos. Recuerda que para explorar estos programas debes mover los deslizadores, que son esos puntos gordos que aparecen en unas guías punteadas.
Un detalle: cuando en esa web se dice "isometrías" se refieren a "movimientos en el plano". Son lo mismo.

Diseña tu mosaico al estilo de Escher

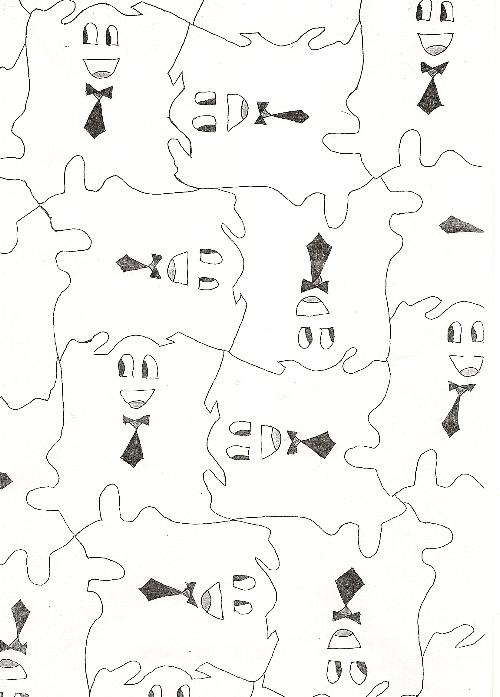
La tarea que tenéis que realizar para el viernes es matemático-artística. Se trata de que diseñéis un mosaico figurativo (las baldosas han de tener forma de persona, animal, planta, etc.) usando la técnica observada por M.C. Escher en los mosaicos de La Alhambra, que después desarrolló con su creatividad. En las hojas repartidas en clase se explica con detalle. En resumen: se parte de un mosaico regular (triángulos equiláteros, cuadrados o hexágonos regulares) y se va alterando la baldosa básica del mosaico según el principio de la equisuperficialidad (lo que quitamos de un lado, lo añadimos en otro). Además, claro está, hay que poner en juego la imaginación en las formas y en el color. El viernes espero maravillarme con vuestras obras de arte...

Para entrar en materia, aquí tenéis algunos mosaicos del maestro Escher. Los tres primeros, a partir de un mosaico con un solo tipo de baldosa:

 

 El siguiente, a partir de un mosaico con dos tipos de baldosas:

El siguiente, a partir de un mosaico con tres tipos de baldosas:

 

Y para terminar, tres ejemplos de mosaicos realizados en cursos pasados por ortros alumnos de 3º, como vosotros:

 

Diario de clase

Escrito por María José:

Hoy en clase de mates, hemos comenzado la clase corrigiendo los ejercicios del día anterior,(pag.212 nº2 / pag.213 nº1,2 / pag.218 del 10-13.
Al acabar, el profesor ha explicado los mosaicos y el símbolo de Deschapi (Schaffli), una forma para decir como son los mosaicos sin necesidad de dibujarlos.
Al acabar de explicar, hemos practicado haciendo ejercicios y por último al final de la clase el profesor nos ha repartido unas fotocopias para diseñar en casa un mosaico.

Encuentra los movimientos

Esta foto corresponde a una yesería mudéjar en el techo de la iglesia del pueblo zaragozano de Trasobares. 

1. ¿Qué movimiento es el que transforma la figura que está centrada en A en la figura centrada en B? 

2. ¿Y el que transforma la figura centrada en A en la figura centrada en C?

En los dos casos, intenta dar cuantos detalles sea posible sobre dichos movimientos.

Diario de clase

Hola soy Manuel

Hoy lo primero el profesor no ha pasado a mirar si habíamos hecho los ejercicios, luego los hemos corregido. Una vez corregidos nos ha explicado como al hacer (componer) dos movimientos iguales o diferentes podía resultar ese mismo movimiento o otro distinto (estudiando varios casos). Por último nos ha mandado unos ejercicios para practicar que son: página 212 el 2 página 213 el 1 y 2 y página 218 del 10 al 13.

Mr. Bean y el giro de 180º

...que convierte el 25 en 52.

Mr. Bean y las simetrías

No os lo perdáis.... :-)

Diario de clase

Hola soy Carlota:

Hoy al empezar la clase, el profesor ha explicado el problema de la semana "El padre, el hijo y el caballo".

Luego ha pasado por las mesas para que le enseñaramos las fotocopias que debíamos hacer en este puente, y las hemos corregido. Después, ha explicado las simetrías axiales y los elementos dobles en una simetría (página 212 del libro).

Para el próximo día hay que hacer de la hoja nº 2 los ejercicios F, G, H, I.

Buen fin de semana.

Fotos enviadas por Alejandro

Las realizó en Cambrils (Tarragona). Las dos primeras son geométricas. Un mosaico regular conocido:

 

Los tres triángulos de la parte superior parecen poder obtenerse unos a partir de los otros mediante giros. ¿Dónde estaría el centro de giro en tal caso? ¿Cuál sería el ángulo de giro? Y aparte: esas letras son de alfabeto cirílico. ¿Tantos rusos hay en Tarragona?

La última no es matemática, pero sí curiosa... allí falta algo ¿no?

Problema de la semana: cuadrados perfectos.

Observa: sólo los números que son cuadrados perfectos tienen un número impar de divisores. ¿Por qué ocurre eso?

1, 4, 9, 16, 25, 36, 49, 64, 81, 100...

 

Se reciben comentarios hasta el jueves 10 de mayo a las 22:00. Entonces se harán visibles, junto a la solución correcta.

Solución al Problema de la semana: el padre, el hijo y el caballo

Recordemos el enunciado:

Un padre y un hijo tienen que recorrer 60 km y disponen de un caballo que trota a 12 km/h, pero que es incapaz de llevar más de una persona a la vez. Consecuentemente, el padre, que anda a 6 km/h, y el hijo, que lo hace a 8 km/h, deben turnarse en el uso del caballo.

Padre e hijo quieren llegar a la vez a su destino. ¿Cómo lo conseguirán?

Ya están visibles los comentarios de Mario, Ángela y Ana que puedes ver aquí. También han llegado escaneadas las respuestas de Iván y María José. Todas bastante trabajadas y bien expresadas. Os felicito por ello.
Iván responde así:

Iván: Tu respuesta es como la de Ana. Igualas los tiempos en movimiento del padre y del hijo, lo cual es imposible pues cuando pare el primero que salió a caballo deberá esperar al caminante que viene por detrás de él. Igualmente, el segundo que coja el caballo deberá esperar un tiempo para dar ventaja al otro que hará caminando el tramo final... es la única forma de que ambos puedan llegar a la vez. En tu ecuación no aparecen esos tiempos de descansos, es como si cuando el primer jinete baja del caballo allí estuviera el otro para cogerlo... algo imposible pues iba más despacio. Incluir los descansos en la ecuación la complicaría mucho, por eso es mejor ir tanteando posibles soluciones teniendo en cuenta los descansos necesarios, como han hecho Mario y Ángela.
Y María José:

María José: confundes las variables. En la primera ecuación llamas x e y a los espacios. Pero en la segunda, llamas x e y a los tiempos. Además, tampoco tienes en cuenta los tiempos de descanso necesarios, como expliqué antes.

En definitiva, las respuestas correctas las dan Mario y Ángela. Mañana os pediré que las expongáis al resto de la clase.

Enseguida, un nuevo problema.

Acertijo... ¿geométrico?

¿Qué es?

La geometría se hace arte

En la historia de las matemáticas los árabes ocupan un papel nada despreciable. A ellos les debemos algo tan fundamental en nuestra cultura como los símbolos de los números tal como los utilizamos en la actualidad, con la aportación del "cero" que llegó directamente desde India hasta Europa. En este capítulo de la serie "Más por menos" veremos cómo la Alhambra de Granada es una de las manifestaciones más importantes del arte geométrico. También, cómo en el siglo XX, el artista holandés M.C. Escher se inspiró en los mosaicos de La Alhambra para desarrollar su obra (una de las hojas de prácticas que os dí el viernes reproduce un mosaico de Escher).